Математическая модель прогноза сезонных продаж с учетом количества клиентов и дефицита продукции на складе.
СОДЕРЖАНИЕ.
Введение.
*1. Расчет тренда, циклической составляющей, сезонности, случайной компоненты, прогноза количества продаж по товарным группам и по ассортиментным позициям.
*1.1 Мультипликативная модель временного ряда.
*1.2 Показатель ошибки и оценка качества прогноза.
*1.3 Ошибка и период прогноза.
*1.3.1 Долгосрочный прогноз и циклическая компонента.
*1.3.2 Доверительные интервалы прогноза.
*1.4 Сезонные индексы.
*1.4.1 Сглаживание средних значений индексов.
*1.4.2 Устаревание индексов.
*1.4.3 Вычисление индексов товаров одной группы.
*2. ARIMA моделирование случайной компоненты.
*2.1 Выбор ARIMA-модели.
*2.1.1 ARMA – процесс (1,0,1).
*2.1.2 Авторегрессия (1,0,0).
*2.1.3 Скользящее среднее (0,0,1).
*2.1.4 Выводы.
*2.2 Ошибка и период прогноза.
*2.3 Параметры ARMA-модели похожих продуктов.
*3. Регрессионный анализ влияния количества клиентов и дефицита продукции на количество продаж.
*3.1 Влияние количества клиентов.
*3.1.1 Вычисление лага и быстроты влияния клиентов.
*3.1.2 Учет клиентов в модели.
*3.1.3 Влияние клиентов на точность прогноза.
*3.2 Влияние дефицита продукции.
*3.2.1 Вычисление лага и быстроты влияния дефицита.
*3.2.2 Невозможность учета дефицита в модели.
*3.3 Выводы.
*4. Полная сезонная ARIMA-модель.
*4.1 Выбор и идентификация ARIMA-модели.
*4.2 Диагностическая проверка.
*4.3 Ошибка и период прогноза.
*4.3 Параметры ARIMA-модели похожих продуктов.
*5. Нахождение оптимального метода описания временного ряда по критерию минимального отклонения прогноза от факта продаж.
*5.1 Усреднение прогнозов разных моделей.
*6. Алгоритмы.
*6.1. Расчеты скользящего среднего, сезонности, тренда.
*6.1.1 Скользящее среднее.
*Скользящее среднее = тренд*цикличность
*6.1.2 Сезонные индексы.
*Сезонный индекс = Данные/Скол.Среднее
*Средний индекс = среднее (Данные/Скол.Среднее) за сезон
*6.1.3 Поправка на сезон.
*Поправка на сезон = Данные/Сезонный индекс
*6.1.4 Тренд.
*6.1.5 Прогноз с поправкой на сезон.
*Прогноз = Тренд*Сезонный индекс
*6.2 Расчеты ARMA-модели случайной компоненты.
*6.3 Учет клиентов.
*6.4 Сезонная ARIMA-модель.
*6.5 Комбинированная модель.
*Цель - анализируя продажи фирмы, торгующей молочными продуктами, построить математическую модель прогноза продаж и на ее основе написать программу прогноза, работающую в электронной таблице Excel. Моделирование сопровождается обоснованием принятия решения с показом числовых результатов и графиков и пошаговым алгоритмом реализации модели на компьютере. Чтобы не прерывать ход рассуждений, алгоритмы вынесены в отдельный раздел в конце отчета. Графики, таблицы, результаты, если не оговорено противное, относятся к творогу. Предполагается, что временные ряды других товаров имеют сходные статистические свойства и могут моделироваться аналогично. Отчет содержит описание 2-х различных моделей: трендовой и ARIMA. В п.1 рассмотрена трендовая модель. Она представляет временной ряд в виде произведения нескольких компонент: тренда, сезонности, цикличности, случайности. В п.2 трендовая модель улучшается за счет моделирования случайной компоненты. В п.3 в трендовую модель включается дополнительная априорная информация о количестве клиентов и дефиците продукции. В п.4 анализируется абсолютно другой подход к моделированию ряда продаж – сезонные ARIMA-процессы Бокса-Дженкинса. В п.5 оба подхода – трендовый и ARIMA объединяются для получения более точных прогнозов. В п.6 описаны алгоритмы решения задач, рассмотренных в п.1-5.
1. Расчет тренда, циклической составляющей, сезонности, случайной компоненты, прогноза количества продаж по товарным группам и по ассортиментным позициям.Обосновывается выбор математической модели временного ряда, предлагается критерий качества модели и показатель ошибки прогноза, обсуждается различная роль циклической компоненты в кратко- и долгосрочном прогнозе, даются рекомендации по уточнению сезонных индексов для товаров, принадлежащих одной группе. Вводится понятие устаревания индексов. Предлагается метод сглаживания индексов, способ автоматического исключения выбросов при вычислении индексов на основании диаграммы рассеяния.
1.1 Мультипликативная модель временного ряда.Для упрощения анализа временной ряд разбивается на несколько независимых компонент: тренд, сезонность, цикличность, нерегулярность. Эти компоненты можно комбинировать различными способами: складывать и умножать. В зависимости от способа сочетаний компонент, модели ряда получили названия аддитивной (при сложении), мультипликативной (при умножении) или смешанной. Данные для творога (код 1010) хорошо описываются мультипликативной моделью:
Данные
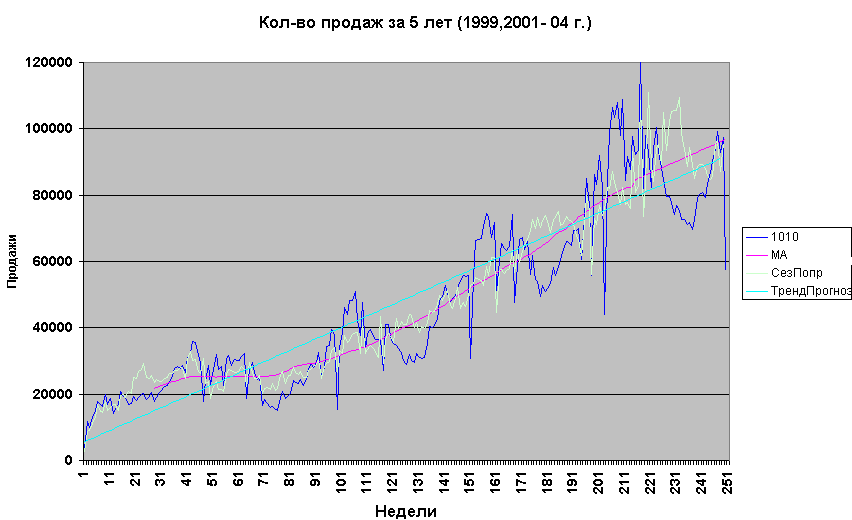
= тренд*цикличность*сезонность*нерегулярностьНа рис.1.1.1 показаны график продаж товара 1010 (синяя линия) за 5 лет. Данные за 2000 год отсутствуют.

Рис.1.1.1 Данные, тренд, сезонность, цикличность.
Хорошо прослеживается линейный рост (тренд) - голубая прямая ТрендПрогноз. Тренд характеризует долговременное поведение ряда. Видны 4 плавных подъема и 3 резких спада (1 неделя января). Повторяющиеся каждый год колебания описывает сезонный компонент, изображенный на рис.1.1.2. Т.к. размах колебаний увеличивается с трендом см.рис.1.1.1, то сезонность нужно умножать на тренд, а не складывать с ним.

Рис.1.1.2 Сезонность.
Хотя на графике сезонности рис.1.1.2 три резких спада продаж (точки 73, 125, 177) в начале года разделены ровно 1 годом (52 недели), в отношении других пиков этого не скажешь. В идеале кривая сезонности должна точно повторяться каждый год. Если посмотреть на выборочную коррелограмму сезонности на рис.1.1.3

Рис.1.1.3 ЧАКФ сезонности.
, то длина нижнего столбца с лагом 52 (соответствующего годовой периодичности) не выходит за границы белого шума (красная штриховая линия), что говорит о слабо выраженной годовой периодичности. Это можно объяснить 2 причинами:
Заметим, что квартальная (лаг=13) и месячная (лаг=4) периодичности на рис.1.1.3 также не видны. Годовая периодичность включает в себя квартальную и месячную. Кроме того, на рис.1.1.2 главные подъемы и спады разделены годовым промежутком, поэтому далее рассматривается только годовая периодичность.
Неопределенность сезонных индексов, следующая из того, что кривая на рис.1.1.2 не строго повторяет себя каждый год, может быть уменьшена привлечением дополнительной информации о похожих товарах (см. п.1.4.3).
Цикличность (вместе с трендом) показана на рис.1.1.1 красной линией MA (moving average – скользящее среднее). Она описывает медленные колебания длительностью более года. На цикличность тоже нужно умножать, чтобы нерегулярность, график которой показан на рис.1.1.4, имела постоянную, а не увеличивающуюся с трендом, дисперсию.
Рис.1.1.4 Нерегулярность.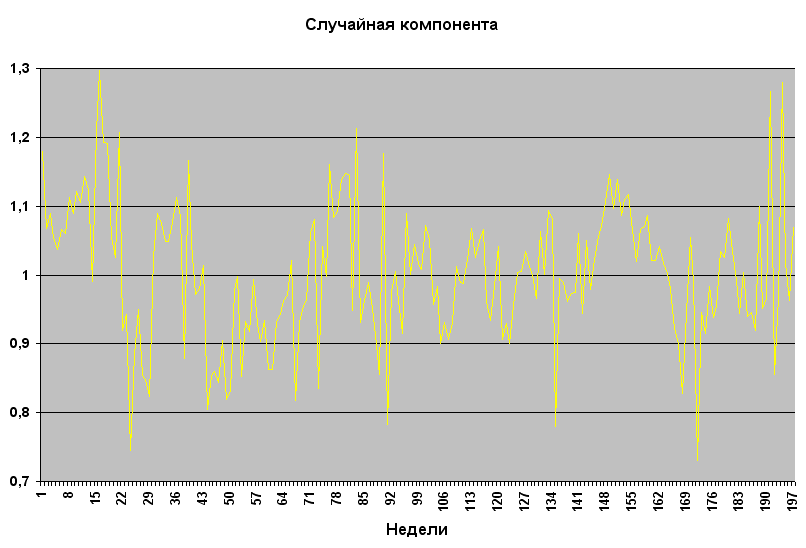
Нерегулярность на рис.1.1.4 в идеале должна быть белым шумом, т.е. данные ряда не должны быть коррелированы (зависимы). Несмотря на кажущуюся непредсказуемость ряда на рис.1.1.4, его структура не совсем случайна. Одной из причин зависимости данных нерегулярной компоненты может быть слабо выраженная сезонность ряда продаж. Анализ структуры нерегулярности и ее влияния на точность прогноза проведен в п.2. Расчеты тренда, сезонности и цикличности приведены в п.6.1.
1.2 Показатель ошибки и оценка качества прогноза.Прогноз и действительные значения ряда отличаются, но каким показателем мерить эти отличия? Среди множества типов ошибок, самой подходящей является абсолютная относительная ошибка - APE:

, где ![]() - данные,
- данные, ![]() - прогноз.
- прогноз.
Среднее значение ошибки APE обозначается MAPE :

имеет ясную интерпретацию – типичная ошибка прогноза равна ![]() *MAPE единиц продукции. Чтобы не возникло дефицита, на складе должно быть кол-во продукции согласно прогнозу ПЛЮС величина средней ошибки. Кроме ясности, MAPE обладает большей устойчивостью к выбросам по сравнению со средней квадратичной ошибкой
*MAPE единиц продукции. Чтобы не возникло дефицита, на складе должно быть кол-во продукции согласно прогнозу ПЛЮС величина средней ошибки. Кроме ясности, MAPE обладает большей устойчивостью к выбросам по сравнению со средней квадратичной ошибкой
 .
.
Следовательно, прогнозы на основе MAPE будут более надежны.
Модель ряда считается хорошей, если ошибка прогноза MAPE мала и остатки ряда:
остатки = данные - прогноз
имеют вид белого шума, т.е. их дисперсия постоянна и они некоррелированы.
1.3 Ошибка и период прогноза.Прогнозы на 1, 2,…, 12 недель вперед вычислялись по мультипликативной модели п.1.1.1 с ошибкой MAPE, описанной в п.1.1.2. Результаты представлены на рис.1.3.1. С увеличением периода прогноза ошибка увеличивается почти
Рис.1.3.1 Ошибка прогноза.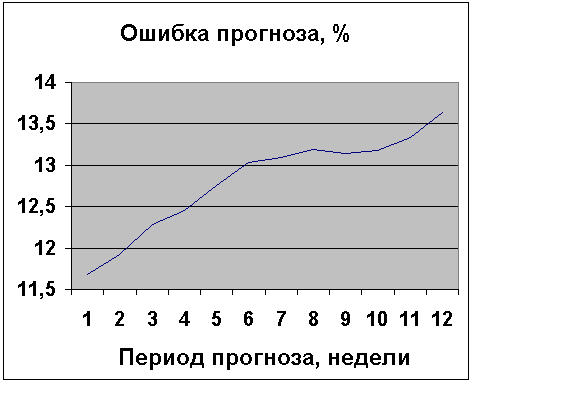
линейно. Средняя величина ошибки MAPE составляет 13%. Величина ошибки получилась большой из-за долгосрочной экстраполяции тренда. Применяя краткосрочную экстраполяцию, MAPE снижается на 2%.
1.3.1 Долгосрочный прогноз и циклическая компонента.
Ошибка прогноза связана с амплитудой колебаний циклической компоненты, показанной на рис.1.3.2.

Рис.1.3.2 Циклическая компонента.
Из графика на рис.1.3.2 видно, что амплитуда колебаний циклической компоненты вокруг среднего значения, равного единице, со временем уменьшается. В последний год (52 точки) она составляла около 5%. Вывод: долговременный (1 год и больше) прогноз не может быть точнее 5%, т.к. невозможно предугадать поведение цикличности на большой промежуток времени вперед. Циклическая компонента, в отличие от тренда, не имеет устойчивого поведения и может быть предсказана только на коротких (1-2 недели) временных интервалах. Отсутствие информации о цикличности, наличие неопределенности в тренде и сезонности увеличивают ошибку с увеличением периода прогнозирования.
1.3.2 Доверительные интервалы прогноза.
Прогноз является важной величиной. Второй по значимости после величины прогноза является его средняя ошибка MAPE. Какой смысл в прогнозе, если его неопределенность (ошибка) слишком велика? Зная прогноз и его ошибку, мы можем с определенной долей уверенности предсказывать границы интервалов будущих продаж. В предположении нормального закона распределения ошибки, границы 95%-ных доверительных интервалов прогноза лежат в ± 2-х стандартных отклонений, равных MAPE. Из рис.1.3.1 следует, что 95% доверительный интервал в среднем по кварталу равен прогноз ± 26%. Вероятность 95% означает, что только 5% фактических значений ряда (каждая 20-ая точка) будет лежать вне доверительных интервалов. Вывод: наряду с прогнозом всегда вычислять его погрешность.
1.4 Сезонные индексы.Сезонные индексы показывают, насколько продажи различаются в разное время года, см. рис.1.4.1. Если в 1-ую неделю индекс равен 0,5, а в 8-ую равен 1,5, то спрос на 8-ой неделе превышает спрос на 1-ой в 1,5/0,5 = 3 раза. Виден большой разброс (дисперсия) индексов вокруг среднего значения. Большая дисперсия подтверждает слабо выраженную сезонность и отсутствие годового пика на коррелограмме, см. рис.1.1.3.
1.4.1 Сглаживание средних значений индексов.
На рис.1.4.1 показаны сезонные индексы для каждого года и среднее значение за 5 лет. Год равен дробному количеству 52,14 недель, но для упрощения расчетов он полагался равным целому числу 52 неделям, а неполная последняя неделя года переносилась на первую неделю следующего. Из рисунка видна
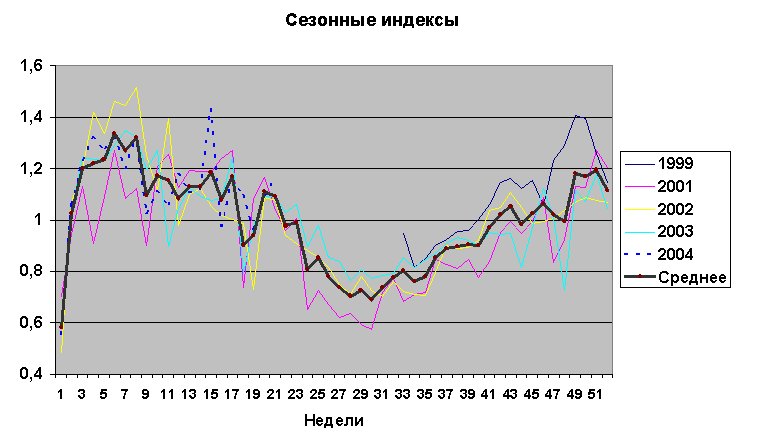
Рис.1.4.1 Сезонные индексы.
сильная изломанность как годовых, так и средних значений индексов (темная линия), которая вызвана случайностью. Сглаживая эту линию, можно повысить точность расчетов. Одним из методов регуляризации является разложение в ряд Фурье и отбрасывание высокочастотных гармоник.
Из рис.1.4.1, видно, что в 1999 году индексы на протяжении 2-ой половины года были выше, чем в последующие годы. А в 15-ую неделю 2004 года индекс неожиданно прыгнул вверх. Это говорит о том, что кривая индексов не стоит на месте, а непрерывно меняется. Изменение вызвано переносом праздников, обновлением ассортимента и т.д. Новые индексы для прогноза имеют большую значимость (вес), чем старые. Существует конечная память, после которой ряд “забывает” свои индексы. Интерпретация устаревания: сегодняшнее изменение в сезонности продаж для прогноза более важно, чем такое же изменение в прошлом году. Отсюда следует, что усреднение индексов по годам нужно брать с весами, уменьшающимися с их возрастом.
Вычисление скорости устаревания индексов.
Пусть темп устаревания – это время, через которое вес индекса снижается вдвое. Сравним точности прогноза с разными темпами устаревания и выберем тот темп, при котором точность прогноза максимальна. Результат расчетов: при 1-недельном прогнозе темп устаревания равен 1 году. Точность прогноза с учетом устаревания увеличивается на 2% по сравнению с прогнозом без устаревания. Вывод: не забывайте включать модель устаревания индексов, если хотите повысить точность прогноза.
1.4.3 Вычисление индексов товаров одной группы.
Когда товар новый или нет достаточных данных для оценки его сезонности, помогает информация о товарах родственной группы. Продукция одного ассортимента имеет одинаковые сезонные индексы. Чтобы это доказать, проанализируем матрицу корреляций индексов для 5 групп различных товаров табл.1.4.1.
Табл.1.4.1 Матрица Rij корреляций индексов.
|
1010 |
1100 |
1300 |
1301 |
1302 |
|
|
1010 |
1 |
||||
|
1100 |
0,40660 |
1 |
|||
|
1300 |
0,63732 |
0,49970 |
1 |
||
|
1301 |
0,73587 |
0,51674 |
0,75513 |
1 |
|
|
1302 |
0,69309 |
0,47284 |
0,52577 |
0,83758 |
1 |
Элементы матрицы показывают, насколько индексы одних товаров связаны с другими. Чем ближе коэффициент корреляции R к 1, тем сильнее связь. Например, товары 1301 и 1302 имеют наибольший R=0,84, значит они должны быть сильно похожи. Например, это может быть творог, но с различной

Рис.1.4.2 График рассеяния индексов товаров 1010 и 1302, R=
0.7.жирностью. Наоборот, товары 1010 и 1100 имеют наименьший R=0,41, значит это товары разного ассортимента. Например, это может быть творог и сметана. Из таблицы видно, что 90% коэффициентов корреляции R больше 0,5. Графики рассеяния подтверждают линейную зависимость индексов рис.1.4.2. Вывод: усредняйте сезонность товаров одного ассортимента, а для новых товаров используйте сезонные индексы похожих товаров.
2. ARIMA моделирование случайной компоненты.Зачем вообще моделировать случайную компоненту (нерегулярность) трендовой модели? Ведь само слово случайная означает, что никакой полезной информации из нее извлечь нельзя. Но в том-то и дело, что она не совсем случайная. В идеале нерегулярность, изображенная на рис.1.1.4, должна иметь вид белого шума. Однако, коррелограмма рис.2.1
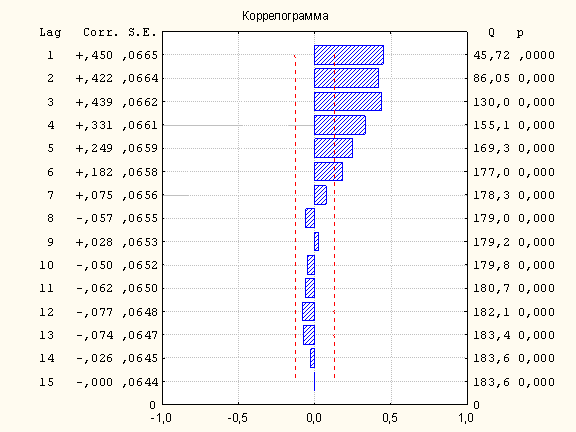
Рис.2.1 Коррелограмма АКФ.
и выборочная коррелограмма рис.2.2
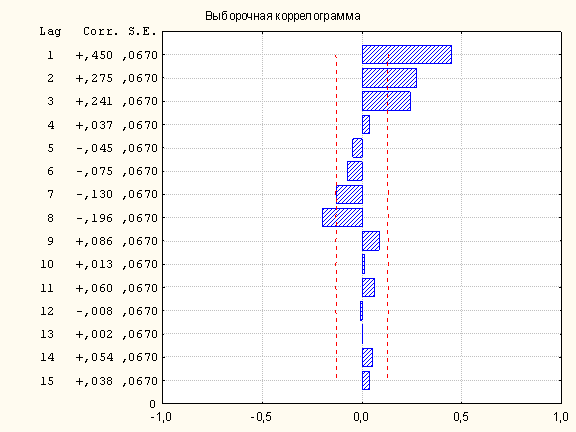
Рис.2.2 Выборочная коррелограмма ЧАКФ.
показывают, что это не так. ЧАКФ (частная автокорреляционная функция) и АКФ белого шума не должны выходить за пределы красной штриховой линии. Но из рисунков 2.1, 2.2 следует, что: 6 первых значений АКФ, 3 первых и 8-ое значение ЧАКФ значимо отличаются от нуля. Значения нерегулярной компоненты оказываются зависимыми. Почему это случилось? Одно из объяснений – недостаточно выраженная сезонность и влияние внешних по отношению к модели, неучтенных факторов. Раз данные нерегулярности зависимы, то можно попытаться их предсказать и, следовательно, увеличить точность прогноза. Из рис.1.1.4 видно, что среднее значение нерегулярности (как и должно быть) равно 1, а стандартное отклонение равно 10%. Интерпретация стандартного отклонения случайного компонента: точность наилучшего прогноза без учета дополнительной информации НЕ МОЖЕТ ЗНАЧИТЕЛЬНО ПРЕВЫСИТЬ 10%. Если бы нерегулярность была белым шумом, то максимум точности был бы равен 10%, но знание структуры нерегулярности и учет дополнительной информации помогает увеличить точность прогноза. Лучше всего с предсказанием нерегулярности справляется ARIMA-моделирование (см.ниже). Учет дополнительной информации обсуждается в п.3.
2.1 Выбор ARIMA-модели.АКФ и ЧАКФ на рис.2.1 и 2.2 не соответствуют ни одному из 3-х основных ARIMA-процессов 1-ого порядка:
, поэтому каждая из 3-х моделей проверялась на точность прогноза, прежде чем был сделан окончательный выбор в пользу одной из них.
2.1.1 ARMA – процесс (1,0,1).Параметры модели Const, p(1), q(1) вычислялись с помощью программы Statistica 6.0 и приведены в табл.2.1.1. Все они значимы, т.к. стандартная ошибка Std.Err много меньше самих параметров Estimate.
Табл.2.1.1 Параметры ARMA.
|
Const. |
p(1) |
q(1) |
|
|
Estimate |
1,0102 |
,86228 |
,53995 |
|
Std.Err. |
,01838 |
,04901 |
,07078 |
Ошибка MAPE 1-недельного прогноза по годовому периоду составила: 7,7%. Таким образом ARMA дала 30% увеличение точности по сравнению с моделью долгосрочного прогноза, см.рис.1.3.1.
2.1.2 Авторегрессия (1,0,0).Параметры модели Const, p(1) приведены в табл.2.1.2. Все они значимы.
Табл.2.1.2 Параметры авторегрессии.
|
Const. |
p(1) |
|
|
Estimate |
1,0056 |
,44993 |
|
Std.Err. |
,01071 |
,06026 |
Ошибка MAPE 1-недельного прогноза по годовому периоду составила: 8,3%.
2.1.3 Скользящее среднее (0,0,1).Параметры модели Const, q(1) приведены в табл.2.1.3. Все они значимы.
Табл.2.1.3 Параметры скользящего среднего.
|
Const. |
q(1) |
|
|
Estimate |
1,0048 |
-,3248 |
|
Std.Err. |
,00814 |
,05545 |
Ошибка MAPE 1-недельного прогноза по годовому периоду составила: 9,2%.
2.1.4 Выводы.Сравнение ошибок 3-х разных моделей в п.2.1-3 позволяет сделать выбор наилучшей ARIMA-модели. Наименьшую ошибку 7,7% дает комбинированная модель регрессии и скользящего среднего ARMA. Алгоритм ARMA –модели описан в п.6.2. Далее рассматриваются результаты моделирования случайной компоненты по ARMA –модели.
2.2 Ошибка и период прогноза.На рис.2.2.1 изображена зависимость MAPE ошибки прогноза от периода прогноза. Сравнивая с рис.1.3.1, можно сделать вывод, что ARMA дает выигрыш в точности прогноза, для всех периодов, но выигрыш распределен неравномерно. Чем меньше период прогноза, тем точнее ARMA-модель, по сравнению с трендовой моделью без учета структуры случайной компоненты.
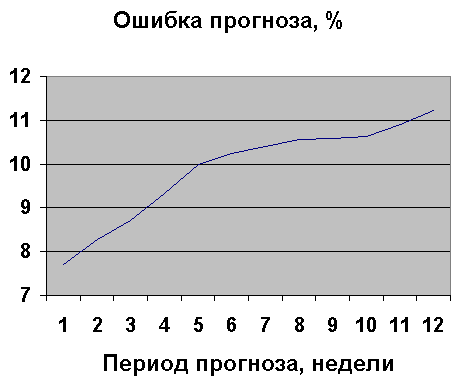
Рис.2.2.1 Ошибка прогноза ARMA.
Среднее по 12-недельному периоду прогноза увеличение точности ARMA-модели случайной компоненты составляет 3%. Вывод: всегда моделируйте случайную компоненту.
2.3 Параметры ARMA-модели похожих продуктов.Представьте, что вы только что начали выпуск нового товара и пока не имеете надежных статистических данных его продаж. Как вычислить неизвестные параметры ARMA? Ответ: так же, как это было сделано для сезонных индексов в п.1.4.3. Нерегулярные составляющие продуктов одного ассортимента должны иметь одинаковую структуру, поэтому параметры ARMA уже известны, если есть данные по аналогичным продуктам. Кроме того, усредняя эти параметры для разных продуктов одного ассортимента, можно улучшить прогноз СРАЗУ ДЛЯ ВСЕХ похожих продуктов.
3. Регрессионный анализ влияния количества клиентов и дефицита продукции на количество продаж.В п.1 был рассмотрен фактор сезонности, без учета которого невозможно делать хорошие прогнозы. Такого рода факторы статистики называют дополнительной или априорной информацией. Если удастся понять, как фактор влияет на интересующую величину (продажи), то можно увеличить точность ее предсказания. Ниже рассматриваются два фактора: количество клиентов и дефицит продукции. Обсуждается количественное влияние их на продажи, способ учета этого влияния и выигрыш в точности прогноза продаж.
3.1 Влияние количества клиентов.
Ясно, что чем больше клиентов, тем больше продаж. Но как найти эту зависимость? Первое, что приходит в голову – построить график рассеяния , см. рис.3.1.1 и найти корреляцию между продажами с сезонной поправкой и клиентами, возможно, с некоторой задержкой во времени (лагом). И действительно, такая корреляция существует, точки группируются вокруг розовой прямой, см. рис.3.1.1, сдвиг = - 24000 (значимость 6%), а наклон = 52,1 (очень высокая значимость 10 -12%), лаг=0,
Рис.3.1.1 График рассеяния продажи-клиенты 2003-04 г, лаг=0.
Доля полной вариации, объясняющей зависимость продаж от клиентов R2=40%. Это означает, что количество клиентов на момент прогноза объясняет 40% изменений продаж. Но нам неизвестно количество клиентов в момент прогноза (в будущем), мы знаем только их количество до этого момента. Попробуем ответить на вопрос: “Зависят ли сегодняшние продажи от количества клиентов в прошлом и, если зависят, то с каким лагом?”.
3.1.1 Вычисление лага и быстроты влияния клиентов.
Построим графики рассеяния для лагов 1, 2 и т.д. Они оказываются похожими на рис.3.1.1 с приблизительно тем же коэффициентом наклона и высокой, но различной значимостью. Выберем лаг, значимость коэффициента наклона которого максимальна (лаг=0 не рассматриваем, т.к., хотя его значимость наибольшая, мы не умеем предсказывать количество клиентов). Как показывает регрессионный анализ, лаг максимальной значимости наклона равен 4, т.е. клиенты влияют на продажи с задержкой в 1 месяц. Хотя значимость влияния клиентов с запаздыванием в 4 недели максимальна, соседние лаги так же высоко значимы. Проведем усреднение по 3-м соседним лагам (4-ый положительный лаг отвечает прогнозу). Результат усреднения:
R2 =42% (увеличился на 25%), сдвиг = - 6,1× 10+4 (значимость 0,064%),
наклон = 72,6 (значимость 2× 10-12 % увеличилась в 200 раз по сравнению с лаг=0).
Интерпретация наклона и лага: каждый дополнительный клиент через месяц увеличивает количество продаж товара на 73 единицы в неделю.
Усреднение дало увеличение и R2, и значимости коэффициента наклона. Интерпретация усреднения: влияние клиентов замедленное, инерционное. Если вы сегодня нашли дополнительного клиента, не потирайте радостно руки и не спешите к начальству требовать повышения зарплаты. Продажи увеличатся, если только этот клиент не уйдет от вас завтра.
Трендовая модель, описанная в п.1,2 дает прогноз сезонных продаж: переменная Прогноз. В п.3.1.1 выяснилось, что 42% изменений продаж можно предсказать с помощью клиентов: переменная Клиенты. Проведем регрессионный анализ зависимости сезонных продаж: переменная СезПродажи от прогноза. Результат: R2=51%, т.е. 51% изменений продаж объясняется прогнозом. И клиенты (R2=42%), и прогноз (R2=51%) , как показала простая регрессия, почти в равной степени влияют на продажи. Проверим важность учета обоих факторов с помощью множественной регрессии:
СезПродажи
= а + b1*Прогноз + b2*Клиенты, где а, b1, b2 - константы, подлежащие определению.
Результат анализа:
R
2=54% (увеличился), сдвиг а=0 (незначим)b1=0,47 (значимость=1,2%), b2=24,5 (значимость=3,5%)
Вывод: учет клиентов увеличивает долю объясненной вариации продаж с сезонной поправкой R2 на 54- 51=3%. Фактор клиентов значимо влияет на сезонные продажи.
3.1.3 Влияние клиентов на точность прогноза.
В п.3.1.2 показано влияние клиентов на прогноз продаж с сезонной поправкой. Но нам нужен прогноз продаж без этой поправки. Увеличение точности прогноза, вызванное клиентами будет меньше 3%, указанных в п.3.1.2. Это объясняется неопределенностью сезонных индексов. Лаг влияния клиентов на продажи, т.е. временная задержка, после которой сказывается действие клиентов равен 4 неделям, см.п.3.1.1. Следовательно, максимальный период прогноза (упреждения), который можно сделать, учитывая информацию о клиентах, равен 4 неделям. В табл.3.1.1 даны коэффициенты множественной регрессии, их значимость, точность прогноза, получаемая без и с учетом клиентов в зависимости от периода прогноза.
Табл.3.1.1 Точность прогноза и коэффициенты регрессии.
|
прогноз, нед. |
Ошибка прогн., % |
Увеличение точности, % |
b 1 |
Значимость b1 |
b 2 |
Значимость b2 |
|
1 |
6,60 |
0,16 |
0,466 |
0,012 |
24,52 |
0,035 |
|
2 |
7,18 |
0,42 |
0,435 |
0,012 |
25,10 |
0,016 |
|
3 |
7,54 |
0,76 |
0,439 |
0,005 |
24,78 |
0,006 |
|
4 |
8,18 |
1,25 |
0,368 |
0,015 |
22,18 |
0,004 |
|
Среднее |
7,38 |
0,65 |
0,43 |
24,2 |
Вывод: с увеличением периода прогноза влияние клиентов на точность прогноза возрастает: дополнительная точность прогноза с клиентами увеличивается от 0,16 до 1,25% с увеличением периода прогноза от 1 до 4-х недель.
На рис.3.1.2 показана зависимость ошибки прогноза от периода прогноза без и с учетом клиентов.
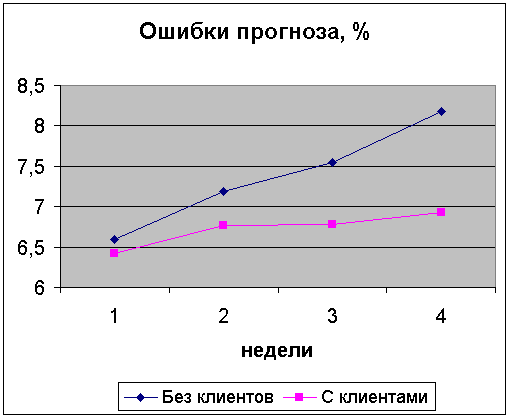
Рис.3.1.2 Ошибка прогноза без и с клиентами.
Замечание.
По сравнению с рис.2.2.1 точность прогноза без клиентов выше на 1%. Повышение точности вызвано не изменением алгоритма, а исключением выброса на 48 неделе 2004 года, который мешал обнаружить влияние клиентов.Эффект увеличения значимости информации о клиентах с увеличением периода прогнозирования объясняется 2-мя причинами:
3.2 Влияние дефицита продукции.
Ясно, что дефицит негативно влияет на продажи. Чтобы описать его влияние, будем действовать аналогично клиентам в п.3.1. Строим график рассеяния продажи-дефицит рис.3.2.1:
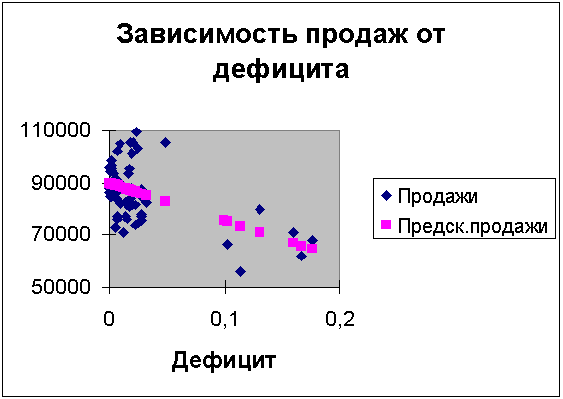
Рис.3.2.1 Продажи-дефицит 2004 г, лаг=0.
Из рисунка следует: чем меньше дефицит, тем выше продажи (что и ожидалось). По сравнению с клиентами, выводы относительно влияния дефицита будут менее надежными, т.к. длина временного ряда дефицита в 2 раза меньше (только за 2004 год). Ответим на вопрос: “Зависят ли сегодняшние продажи от дефицита в прошлом и, если зависят, то с каким лагом?”.
3.2.1 Вычисление лага и быстроты влияния дефицита.
Действуем аналогично клиентам см.п.3.1.1. Построим графики рассеяния сезонные продажи-дефицит для лагов 1, 2 и т.д. Они оказываются похожими на рис.3.2.1 с приблизительно тем же коэффициентом наклона и высокой, но различной значимостью. Выберем лаг, значимость коэффициента наклона которого максимальна. Как показывает регрессионный анализ, лаг максимальной значимости наклона равен 3, т.е. дефицит влияет на продажи с задержкой в 3 недели. Хотя значимость влияния дефицита с запаздыванием в 3 недели максимальна, соседние лаги так же высоко значимы. Но, в отличие от клиентов, усреднение по соседним лагам, не приводит к росту R2 и значимости наклона. Интерпретация отсутствия усреднения: продажи реагируют на дефицит быстрее, динамичнее, чем клиенты. Если вы сегодня снизили дефицит продукции, смело идите к начальству за прибавкой к зарплате. Ровно через 3 недели продажи увеличатся.
Простая линейная регрессия зависимости продаж с сезонностью от дефицита дает: R2=30%. Клиенты объясняют изменение продаж на 42-30=12% больше, чем дефицит. Вывод: нужно в первую очередь искать новых клиентов, а не уменьшать дефицит.
сдвиг = 9,1× 10+4 (значимость 6× 10-53),
наклон = - 1,36× 10+5 (значимость 7× 10-6 ). Интерпретация наклона: каждый дополнительный процент дефицита через 3 недели уменьшает количество продаж товара на 1360 единиц в неделю.
3.2.2 Невозможность учета дефицита в модели.
Добавим к Прогнозу и Клиентам 3-ю независимую переменную Дефицит и проверим ее важность с помощью множественной регрессии для 1-недельного прогноза:
СезПродажи
= а + b1*Прогноз + b2*Клиенты + b3*Дефицит, где а, b1, b2, b3 - константы.
Результат: R2=54% (не изменился по сравнению с п.3.1.2)
а=0 (значимость=0,7 незначим)
b1=0,47 (значимость=0,012) b2=27,1 (значимость=0,03)
b3=0 (0,54 незначим)
Вывод: включение дефицита не увеличило процент объясненной вариации сезонных продаж R2, а коэффициент наклона дефицита b3 незначим. После учета прогноза и количества клиентов взаимосвязи между дефицитом продукции и сезонными продажами нет. Как же так? Простая регрессия показала, что дефицит влияет на продажи, а множественная показала, что нет. Проверим линейную зависимость дефицита от прогноза и клиентов. Парные коэффициенты корреляции дефицит-прогноз R=52%, дефицит-клиенты R=59% большие, следовательно, дефицит линейно зависит от обоих параметров. Конечно, не следует думать, будто дефицит на самом деле связан с прогнозом и клиентами. Объяснений отсутствия влияния дефицита может быть два:
Б
ольшие периоды прогноза.В п.3.2.2 показано, что дефицит не влияет на 1-недельный прогноз сезонных и, тем более, несезонных продаж. Но в п.3.1.3 влияние клиентов на прогноз с увеличением его периода возрастало. Возможно, с увеличением периода прогноза учет дефицита тоже станет важным? Проверим это предположение. Лаг дефицита, т.е. временная задержка, после которой сказывается действие дефицита, равен 3 неделям, см.п.3.2.1. Следовательно, максимальный период прогноза с учетом дефицита равен 3 неделям. В табл.3.2.1 даны коэффициенты множественной регрессии с учетом дефицита и их значимость.
Табл.3.2.1 Коэффициенты регрессии.
|
прогноз, нед. |
b 1 |
Значимость b1 |
b 2 |
Значимость b2 |
b 3 |
Значимость b3 |
|
1 |
0,48 |
0,012 |
27,1 |
0,030 |
26720 |
0,54 |
|
2 |
0,44 |
0,011 |
28,0 |
0,012 |
40410 |
0,45 |
|
3 |
0,46 |
0,004 |
26,1 |
0,005 |
47420 |
0,42 |
|
Среднее |
0,46 |
27,1 |
38200 |
Из таблицы видно, что влияние дефицита с увеличением периодом прогноза растет, но везде значимость b3>0,05, т.е. коэффициент наклона дефицита незначим. Вывод: дефицит влияет на продажи см.п.3.2.1, но у нас нет достаточного количества данных, чтобы учесть это влияние.
Количество клиентов и дефицит продукции значимо влияют на продажи, но их влияние различно. Влияние клиентов замедленное и мягкое, дефицита – быстрое и жесткое. Клиенты объясняют на 12% больше вариаций продаж и данных по клиентам в 2 раза больше (2 года против 1 года для дефицита), поэтому удалось вычислить и количественное влияние клиентов на продажи, и результативно учесть это влияние в прогнозе продаж. Количественное влияние дефицита на продажи получить удалось, но для учета этого влияния в прогнозе не хватило данных.
4. Полная сезонная ARIMA-модель.
Выше, в п.1-3 была рассмотрена трендовая модель прогноза продаж, основанная на анализе тренда и сезонных индексов. В настоящем разделе рассматривается другая – ARIMA модель прогноза продаж. Спрашивается: зачем нужна еще одна модель? Существует, по крайней мере, два ответа на этот вопрос:
В п.2 ARIMA-подход использовался, но только для моделирования случайной компоненты. Трендовая модель по сравнению с ARIMA имеет следующие преимущества:
Сезонные ARIMA-модели, в отличие от трендовых, не разбивают исходный временной ряд на отдельные компоненты: тренд, сезонные индексы и случайную компоненту, а рассматривают его как единое целое.
4.1 Выбор и идентификация ARIMA-модели.
Сезонная мультипликативная модель обозначается так: (p,d,q)´ (ps,ds,qs)
, где p - авторегрессия
d - разность
q - скользящее среднее
приставка s - для сезонной компоненты
Для применения ARIMA ряд должен быть стационарным. Ряд продаж рис.1.1.1 имеет тренд, значит он нестационарен. Для превращения ряда в стационарный требуется взятие разностей ряда d и, возможно, сезонных разностей ds. Иными словами, чему равны: d и ds? Построим графики автокорреляций исходного ряда z, ряда с первыми разностями Ñ z, ряда с сезонными разностями Ñ 52z, ряда с двойными разностями Ñ Ñ 52z. Автокорреляции z и Ñ 52z велики для всех лагов и не затухают, см. рис.4.1.1
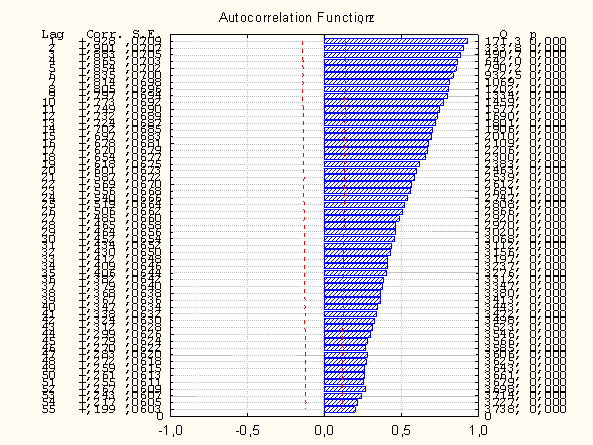
Рис.4.1.1 Автокорреляция продаж, z.
Автокорреляции рядов Ñ z ,Ñ Ñ 52z похожи: большие значение только для лага=1
и 52, см.рис.4.1.2
Рис.4.1.2 Автокорреляция
Выберем из 2-х вариантов Ñ z ,Ñ Ñ 52z двойные разности Ñ Ñ 52z , т.к. оператор Ñ 52 описывает присутствующий в нашей модели долгосрочный тренд. Автокорреляция ,Ñ Ñ 52z удовлетворяет модели скользящего среднего: (0,1,1)´ (0,1,1)52 первого порядка. 190 автокорреляций Ñ Ñ 52z распределены почти по нормальному закону, см.рис.4.1.3:

Рис.4.1.3 Распределение автокорреляций Ñ Ñ
52z.за исключением 2-х больших отрицательных значений: -0,5, -0,4.
Вычислим параметры модели скользящего среднего (0,1,1)´ (0,1,1)52, табл.4.1.1:
Табл. 4.1.1 Параметры скользящего среднего.
|
Const. |
q(1) |
Qs(1) |
|
|
Estimate |
-6,788 |
,64545 |
,42602 |
|
Std.Err. |
114,19 |
,05540 |
,08651 |
Const. не является значимой, поэтому положим Const=0. Остальные параметры значимы. Вывод: модель скользящего среднего (0,1,1)´ (0,1,1)52 не противоречит данным продаж.
Проверим адекватность модели с помощью анализа остаточных ошибок (остатков). На рис.4.2.1 показаны автокорреляции 230 остатков:Рис.4.2.1 Автокорреляции остатков.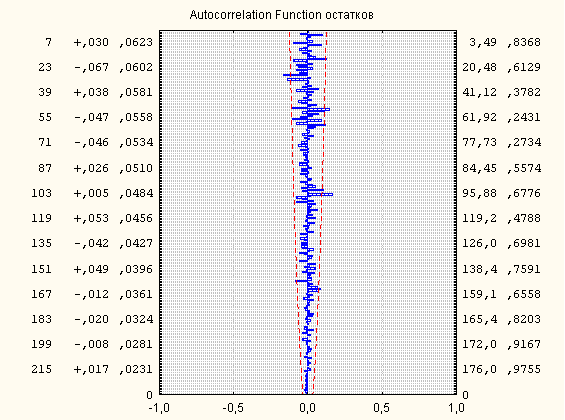
Есть небольшие выходы некоторых значений автокорреляций остатков за границы белого шума (красная штриховая линия), но их мало. На рис.4.2.2 показано распределение остатков:
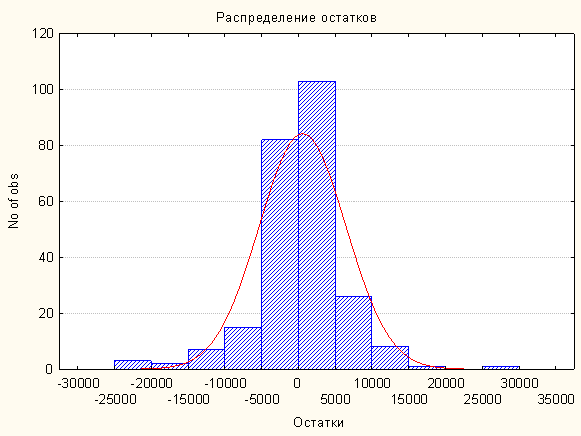
Рис.4.2.2 Распределение остатков.
Из рисунка видно, что среднее значение, как и положено, равно 0, а распределение почти (за исключением крайних значений) нормальное. Вывод: проверка остатков подтверждает адекватность выбранной модели.
На рис.4.3.1 показана ошибка прогноза MAPE сезонной ARIMA-модели в зависимости от периода прогноза (упреждения).
Рис.4.3.1 Зависимость ошибки от периода прогноза.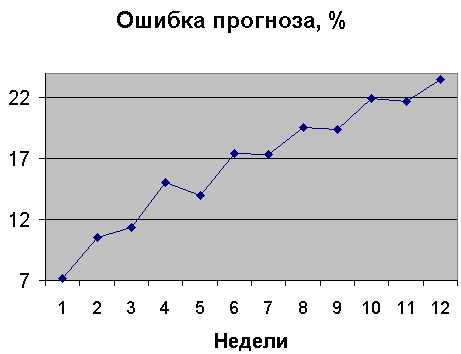
По сравнению с трендовой моделью рис.2.2.1, точность прогноза везде, кроме 1-ой недели, ниже. Как и в трендовой модели, чем дальше вперед мы заглядываем, тем, в среднем, больше ошибка прогноза. Однако, ошибки для нечетных 5, 7, 9, 11 недель меньше, чем для предыдущих четных недель. Это особенности ARIMA-модели. В отличие от трендовой, ARIMA-модель хуже прогнозирует резкие всплески. Например, ошибка MAPE 2-х недельного прогноза на 1-ую неделю 2004 г. (рис.1.1.1, точка 203, очень резкий спад) для ARIMA 72%, для Тренда 4%. Вывод: точность ARIMA-модели для 1-ой недели сравнима, а для остальных - хуже трендовой модели.
4.3 Параметры ARIMA-модели похожих продуктов.
Выводы, сделанные относительно параметров случайной компоненты п.2.3, полностью распространяются на параметры сезонной ARIMA-модели. Если вы выпустили на рынок новый продукт или отсутствуют репрезентативные статистические данные продаж товара, используйте параметры ARIMA-модели товаров схожего ассортимента.
В п.2, 3 была рассмотрена трендовая модель прогноза, в п.4 сезонная ARIMA-модель. Какую из 2-х моделей выбрать? Сравнение прогнозов п.4.3 трендовой и сезонной ARIMA моделей показывает, что долгосрочное (далее 1-ой недели) прогнозирование точнее выполняет трендовая модель. Означает ли это, что заглядывая больше чем на одну неделю вперед, нужно пользоваться только трендовой моделью?
5.1 Усреднение прогнозов разных моделей.
У нас есть две независимые оценки продаж - трендовая и ARIMA. Мы знаем типичные ошибки (стандартные отклонения) каждой из них, см. рис.2.2.1 и рис.4.3.1. Усредняя прогнозы 2-х моделей с весами, обратно пропорциональными их стандартным отклонениям, получим прогноз с наименьшей ошибкой, рис.5.1.1.
Рис.5.1.1 Ошибки прогноза MAPE разных моделей.
Из рис.5.1.1 видно, что точность прогнозов ARIMA и Тренда ниже точности комбинированной модели, обозначенной на рисунке Среднее всюду, кроме прогноза на 4 недели вперед. Из рисунка видно, что ARIMA на 4-ой неделе имеет сильный всплеск погрешности прогноза, который и вызвал ухудшение точности комбинированной модели. Вывод: всегда использовать комбинированную модель.
Выписаны алгоритмы расчета, пригодные для реализации на компьютере.
6.1. Расчеты скользящего среднего, сезонности, тренда.
Тренд и сезонные индексы нужны для преобразования ряда в стационарный, т.е. независящий от времени. Вначале вычисляют скользящее среднее.
Годовая периодичность равна 52, поэтому берем текущее значение ряда, складываем с соседними значениями (25 слева и 25 справа) и добавляем половину от 26 соседей с каждой стороны. Делим сумму на 52. Полученное значение есть скользящее среднее. Оно отсутствует для 26 первых и последних членов ряда и характеризует произведение 2-х компонент:
Скользящее среднее = тренд*цикличность
График скользящего среднего показан на рис.1.1.1 красной линией MA и представляет собой сглаженный ряд данных.
Делим данные ряда на скользящее среднее (см.п.5.1.1):
Сезонный индекс = Данные/Скол.Среднее
График сезонных индексов показан на рис.1.1.2. Потом усредняем полученное значение:
(Данные/Скол.Среднее) за сезонГрафик средних сезонных индексов показан на рис.1.4.1. Далее везде используем средние сезонные индексы, опуская слово средние.
Делим значение ряда на сезонные индексы, получая значение ряда с поправкой на сезонность:
Поправка на сезон = Данные/Сезонный индекс
График ряда с поправкой на сезонность показан на рис.1.1.1 зеленой линией СезПопр.
Прямую линию тренда рис.1.1.1, голубая линия ТрендПрогноз получают с помощью линейной регрессии ряда с поправкой на сезон (п.6.1.3) методом наименьших квадратов:
Долгоср.тренд = a + b× tпрогн
, где tпрогн – номер недели прогноза
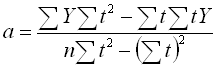 - коэффициент сдвига
- коэффициент сдвига
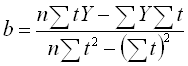 - коэффициент наклона
- коэффициент наклона
Y - значение ряда с поправкой на сезон,
n - полная длина ряда, количество недель
Краткосрочный прогноз тренда отличаются от долгосрочного сдвигом a. Сначала усредняются сезонные продажи за год, n=52:
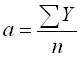 - коэффициент сдвига
- коэффициент сдвига
, потом добавляется наклон долгосрочного тренда:
Краткосрочн.тренд = a + b×
(n/2 + tпрогн)6.1.5 Прогноз с поправкой на сезон.
Окончательное значение прогноза (без учета циклической компоненты) получают умножением тренда на сезонный индекс:
Прогноз = Тренд*Сезонный индекс
6.2 Расчеты ARMA-модели случайной компоненты.
Расчет нерегулярной компоненты на 1 неделю вперед выполняется по формуле:
прогноз(t+1) = Const + p(1)*значение(t) – q(1)*шум(t)
(6.1), где t – текушая (последняя) неделя
p(1)
- параметр авторегрессииq(1)
- параметр скользящего среднегоConst =
1 – p(1)значение
– значение нерегулярностишум
– значение шумаВременной ряд шума может быть получен рекуррентным способом. Положим значение шума в отдаленном (порядка t–10) прошлом равным 0. Вычислим последовательно значение прогноза по формуле (6.1) вплоть до момента t. Значение шума для времен: t–9,t-8,¼ ,t вычисляется по формуле:
шум(t) = значение(t) - прогноз(t) (6.2)
Расчет нерегулярной компоненты на n недель вперед выполняется по формуле:
прогноз(t+n) = Const + p(1)*прогноз(t+n-1) (6.3)
Для этого сначала по формуле (6.1) вычисляется прогноз на 1 неделю вперед. Этот прогноз подставляется в формулу (6.3), чтобы получить прогноз на 2 недели вперед. 2-х недельный прогноз опять подставляется в (6.3), чтобы получить прогноз на 3 недели вперед и т.д.
Формулу для коррекции сезонных продаж см.п.3.1.2. Максимальный период прогноза, учитывающий количество клиентов равен 4 неделям. Необходимо усреднение клиентов по соседним лагам.
Прогноз продаж z(1) на 1 неделю вперед:
![]()
, где zt - фактические продажи в момент t
![]() - параметр скользящего среднего,
- параметр скользящего среднего,
![]() - параметр сезонного скользящего среднего
- параметр сезонного скользящего среднего
t - текущая неделя
at - абсолютная ошибка прогноза, равная: ![]()
Прогноз продаж z(n) на n>1 недель вперед:
![]()
Прогноз комбинированной модели равен:
комби-прогноз = (ошибка_ARIMA * Тренд-прогноз +
ошибка_Тренд * ARIMA-прогноз)/(ошибка_ARIMA+ошибка_Тренд)
, где ошибка означает ошибку MAPE соответствующей модели для заданного упреждения прогноза.